Too Much Xor Codechef Solution in C++| AskTheCode

Team ATC
Jun 20, 2021
3 min read

Codechef June Cook-Off 2021 Solution | Too Much Xor (TOOXOR) solution in C++ | AskTheCode

Problem:

Chef calls a sequence of integers A1,A2,…,ANgood if it satisfies the following

conditions:

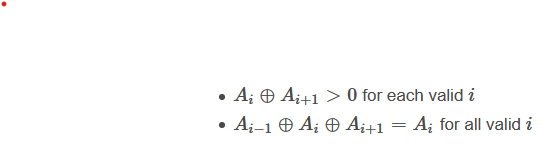
In particular, any sequence with length 1 is good and any sequence of length 2

which satisfies the first condition is good.

Here, ⊕ denotes the bitwise XOR operation.

Chef gives you a sequence A1,A2,…,AN. You may perform the following operation on the sequence any number of times (possibly 0): choose 3 pairwise distinct valid indices a, b and c and change Ac to Aa⊕Ab. Note that this means the operation can only be performed if N≥3.

Chef is asking you to make the sequence good using at most 3⋅N operations or report that it is impossible. Note that you do not have to minimise the number of performed operations.

Input:

The first line of the input contains a single integer T denoting the number of test cases. The description of T test cases follows.
The first line of each test case contains a single integer N.
The second line contains N space-separated integers A1,A2,…,AN.

Output:

For each test case:

If it is impossible to change the given sequence into a good sequence using at most 3⋅N operations, print a single line containing the integer −1.
Otherwise, first, print a line containing a single integer M (0≤M≤3⋅N) ― the number of operations you want to perform.
Then, print M lines describing these operations in the order in which you want to perform them. For each i (1≤i≤M), the i-th of these lines should contain three space-separated integers ai, bi and ci (pairwise distinct; 1≤ai,bi,ci≤N) ― the indices on which the i-th operation is performed.

If there are multiple solutions, you may find any one of them.

Sample Input:

Sample Output:

EXPLANATION:

Example case 1: The sequence is already good, so performing 0 operations is a valid solution.

Example case 2: The sequence cannot be made good using at most 3⋅N operations.

Example case 3: We can make the sequence good by performing the 4 operations shown on the output, in this order. Note that the initial sequence is also good, so performing 0 operations is also a valid solution.

Example case 4: The sequence does not satisfy the first condition and since N=2, we cannot perform any operations on it.

Code:

#include <bits/stdc++.h>
 
#define mod 1000000007
#define fain(arr) for(ll i=0;i<n;i++)cin>>arr[i];
#define all(x) x.begin(),x.end()
#define SPEED ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
#define bugv(n1) if(DEBUG)cout<<#n1<<" is "<<n1<<'\n';
#define buga(A) cout<<#A<<" is :"<<endl ; for(auto x:A)cout<<x<<" "; cout<<endl;
#define FILE freopen("input.txt","r",stdin);
#define rep(i, begin, end) for (__typeof(end) i = (begin) - ((begin) > (end)); i != (end) - ((begin) > (end)); i += 1 - 2 * ((begin) > (end)))
#define endl '\n'
#define ll long long 
#define pii pair<ll,ll>
#define pll pair<long long ,long long >
#define pi acos(-1)
#define sz(x) ((ll)x.size())
#define clr(x) memset(x, 0, sizeof(x))
#define init(x, a) memset(x, a, sizeof(x))
#define DEBUG true
using namespace std;
 
 
int main(){
	// FILE;
	SPEED;
	ll t;
	cin>>t;
	// t=1;
	while(t--)
	{ 
		ll n;
		cin>>n;

		ll arr[n];
		fain(arr);

		if(n==1){
			cout<<0<<endl;
			continue;
		}
		else if(n==2){
			if((arr[0]^arr[1])!=0){
				cout<<0<<endl;
			}
			else{
				cout<<-1<<endl;
			}
			continue;
		}
		else if(n==3){
			bool poss = true;

			for(ll i=1;i<3;i++)
				if((arr[i]^arr[i-1])==0)
					poss=false;

			if((arr[0]^arr[1]^arr[2])!=arr[1]){
				poss=false;
			}

			if(poss){
				cout<<0<<endl;
			}
			else{
				
				vector<vector<int>> op;
				for(int i=0;i<3;i++){

						int brr[3];
						for(int j=0;j<3;j++)brr[j]=arr[j];

					ll allxor = arr[0]^arr[1]^arr[2];

					brr[i]=allxor^brr[i];

					bool poss = true;

					for(ll pp=1;pp<3;pp++)
						if((brr[pp]^brr[pp-1])==0)
							poss=false;

					if((brr[0]^brr[1]^brr[2])!=brr[1]){
						poss=false;
					}

					vector<int> xxx = {0,2,1};
					for(int pp=0;pp<3;pp++){
						if(xxx[pp]==i){
							swap(xxx[pp],xxx[2]);
							break;
						}
					}

					if(poss){
						op.push_back(xxx);
						break;
					}

				}

				if(op.size()>0){

					cout<<op.size()<<endl;

					for(auto x:op){
						cout<<x[0]+1<<" "<<x[1]+1<<" "<<x[2]+1<<endl;
					}
				}
				else{
					cout<<-1<<endl;
				}

			}
		}
		else{


			if(arr[0]!=0)
			{

				vector<vector<ll>> op;

				op.push_back({0,1,2});
				op.push_back({0,1,3});
				op.push_back({2,3,1});

				for(ll i=2;i<n;i++){
					if(i%2==0){
						op.push_back({0,1,i});
					}
					else{
						op.push_back({0,2,i});
					}
				}

				cout<<op.size()<<endl;

				for(auto x:op){
					cout<<x[0]+1<<" "<<x[1]+1<<" "<<x[2]+1<<endl;
				}
		  }
		  else{
		  	 	
		  	 	vector<vector<ll>> op;
		  	   int nzi=-1;
		  	   int ii=0;
		  	   for(auto x:arr){
		  	   	    if(x!=0){
		  	   	    	nzi=ii;
		  	   	    	break;
		  	   	    }
		  	   	    ii++;
		  	   }

		  	   if(nzi==-1){
		  	   	   cout<<-1<<endl;

		  	   }
		  	   else{

		  	   		if(nzi!=1)
		  	   		op.push_back({0,nzi,1});

		  	   		op.push_back({0,1,3});
		  	   		op.push_back({1,3,2});

                   for(ll i=4;i<n;i++){
					if(i%2==1){
						op.push_back({0,1,i});
					}
					else{
						op.push_back({0,2,i});
					}
				   }

				   cout<<op.size()<<endl;

				for(auto x:op){
					cout<<x[0]+1<<" "<<x[1]+1<<" "<<x[2]+1<<endl;
				}

		  	   }

		  }

		}
    }
 
}

Too Much Xor Codechef Solution in C++| AskTheCode

Recent Posts

Comments