Madoka and Ladder Decomposition - Codechef July Long Challenge Solution
- Team ATC

- Jul 4, 2021
- 10 min read
Updated: Jul 15, 2021
Codechef July Long Challenge 2021 Solution | Madoka and Ladder Decomposition solution | ATC
Problem:
Madoka was given a tree on her coming of age, and not a simple one, but a rooted tree of n vertices with a root at the vertex with the number 1.
For all i≥2, let Pi (1≤Pi≤i−1) be the parent of the vertex i. Let's define the depth array h as follows: h1=1, and hi=hPi+1 for all i≥2.
The subtree of a vertex u, denoted S(u), is defined as the set of vertices v such that the unique path from 1 to v contains u. Also, we define
valu = max {h(v) : v ∈ S(u)}.
A tree is divided into paths by a ladder decomposition if each vertex is located on exactly one path, and each vertex u with at least one child lies in the same path as its child v with the maximum valv, and if there are several such vertices, then the vertex with the minimum number is selected.
Madoka defines the beauty of a tree in the following way. Let the ladder decomposition of the path lengths be L1,…,Lk, then the beauty of the tree is L21+L22+⋯+(L^2)k
For each i (1≤i≤n), your task is to calculate the beauty of the tree formed by the first i vertices.
Input:
The first line contains an integer T - the number of test cases. Then T test cases follow.
The first line of each test case contains a single integer n - the size of the tree.
The second line contains n−1 integers P2,…,Pn.
Output:
For each test case, print in a separate line a single integer - the answer to the problem.
Sample Input:
2
6
1 2 1 4 3
12
1 2 1 4 4 6 2 8 5 6 11Sample Output:
0 1 4 4 5 10
0 1 4 4 5 5 10 10 13 14 14 21EXPLANATION:
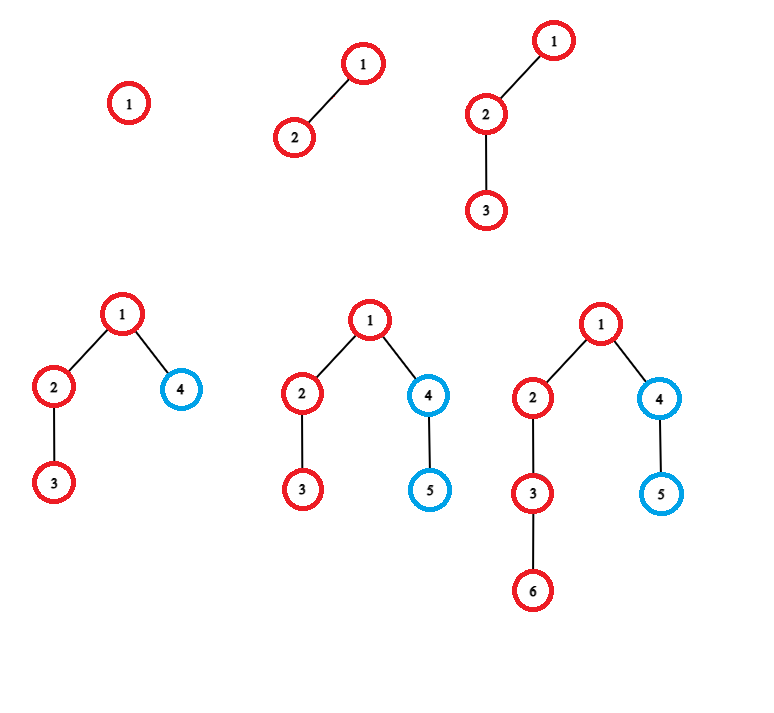
Code:
#include <bits/stdc++.h>
using namespace std;
#define _USE_MATH_DEFINES
struct rooted_tree {
vector<vector<int>> adj;
vector<int> parent, depth, subtree, start, preorder, in, out;
const vector<int>& operator [] (int i) const { return adj[i]; }
rooted_tree(const vector<vector<int>>& adj_list, int root): adj(adj_list),
parent(adj.size(), -1), depth(adj.size()), subtree(adj.size()), start(adj.size()),
in(adj.size()), out(adj.size()) {
preorder.reserve(adj.size());
build(root, -1, 0);
}
rooted_tree(vector<vector<int>>&& adj_list, int root): adj(move(adj_list)),
parent(adj.size(), -1), depth(adj.size()), subtree(adj.size()), start(adj.size()),
in(adj.size()), out(adj.size()) {
preorder.reserve(adj.size());
build(root, -1, 0);
}
bool is_ancestor_of(int anc, int v, bool strict = true) const {
if (strict) return in[anc] < in[v] && out[anc] > out[v];
else return in[anc] <= in[v] && out[anc] >= out[v];
}
private:
int build(int u, int par, int idx) {
in[u] = idx++;
start[u] = (int)preorder.size();
preorder.push_back(u);
parent[u] = par;
subtree[u] = 1;
if (par != -1) {
depth[u] = depth[par] + 1;
vector<int>::iterator it = find(adj[u].begin(), adj[u].end(), par);
if (it != adj[u].end()) {
adj[u].erase(it);
}
}
for (int v : adj[u]) {
idx = build(v, u, idx);
subtree[u] += subtree[v];
}
out[u] = idx++;
return idx;
}
};
template <class DS, typename Query_t>
struct range_query_tree : rooted_tree {
DS range_ds;
vector<int> top; // top of heavy chains
range_query_tree(const vector<vector<int>>& adj_list, int root):
rooted_tree(adj_list, root), range_ds((int)adj.size()), top(adj.size()) {
preorder.clear();
top[root] = root;
build(root, 0);
}
range_query_tree(vector<vector<int>>&& adj_list, int root):
rooted_tree(move(adj_list), root), range_ds((int)adj.size()), top(adj.size()) {
preorder.clear();
top[root] = root;
build(root, 0);
}
int ancestor(int u, int k) const {
if (k < 0) throw invalid_argument("tried to find the kth ancestor where k < 0");
if (k > depth[u]) return -1;
while (true) {
int len = depth[u] - depth[top[u]] + 1;
if (k < len) {
return preorder[start[u] - k];
}
u = parent[top[u]];
k -= len;
}
}
int lca(int u, int v) const {
while (top[u] != top[v]) {
if (depth[top[u]] < depth[top[v]]) swap(u, v);
u = parent[top[u]];
}
return depth[u] < depth[v] ? u : v;
}
int distance(int u, int v) const {
int c = lca(u, v);
return depth[u] + depth[v] - 2 * depth[c];
}
int kth(int u, int v, int k) const {
int c = lca(u, v);
int up = depth[u] - depth[c];
int down = depth[v] - depth[c];
if (k <= up) {
return ancestor(u, k);
} else {
return ancestor(v, up + down - k);
}
}
template <class... Args>
void update_point(int u, const Args&... args) {
range_ds.update_point(start[u], args...);
}
template <class... Args>
Query_t query_point(int u, const Args&... args) {
return range_ds.query_point(start[u], args...);
}
template <class... Args>
void update_subtree(int u, const Args&... args) {
range_ds.update_range(start[u], start[u] + subtree[u] - 1, args...);
}
template <class... Args>
Query_t query_subtree(int u, const Args&... args) {
return range_ds.query_range(start[u], start[u] + subtree[u] - 1, args...);
}
template <class... Args>
int search_subtree(int u, const Args&... args) {
int idx = range_ds.search_left(start[u], start[u] + subtree[u] - 1, args...);
return idx < range_ds.lim ? preorder[idx] : -1;
}
template <class... Args>
void update_non_subtree(int u, const Args&... args) {
range_ds.update_range(0, start[u] - 1, args...);
range_ds.update_range(start[u] + subtree[u], subtree[preorder[0]] - 1, args...);
}
template <class... Args>
Query_t query_non_subtree(
int u, function<Query_t(Query_t, Query_t)> merge, const Args&... args) {
return merge(
range_ds.query_range(0, start[u] - 1, args...),
range_ds.query_range(start[u] + subtree[u], subtree[preorder[0]] - 1, args...));
}
template <class... Args>
int search_non_subtree(int u, Args... args) {
int idx = range_ds.search_left(0, start[u] - 1, args...);
if (idx < range_ds.lim) return preorder[idx];
idx = range_ds.search_left(start[u] + subtree[u], subtree[preorder[0]] - 1, args...);
return idx < range_ds.lim ? preorder[idx] : -1;
}
template <class... Args>
int update_path(int u, int v, bool include_lca, const Args&... args) {
while (top[u] != top[v]) {
if (depth[top[u]] < depth[top[v]]) swap(u, v);
range_ds.update_range(start[top[u]], start[u], args...);
u = parent[top[u]];
}
if (include_lca || u != v) {
if (depth[u] < depth[v]) swap(u, v);
range_ds.update_range(start[v] + !include_lca, start[u], args...);
}
return v;
}
template <class Combine, class... Args>
Query_t query_path(int u, int v, bool include_lca, Query_t res,
const Combine& merge, const Args&... args) {
while (top[u] != top[v]) {
if (depth[top[u]] < depth[top[v]]) swap(u, v);
res = merge(res, range_ds.query_range(start[top[u]], start[u], args...));
u = parent[top[u]];
}
if (include_lca || u != v) {
if (depth[u] < depth[v]) swap(u, v);
res = merge(res, range_ds.query_range(start[v] + !include_lca, start[u], args...));
}
return res;
}
template <class... Args>
int search_path(int u, int v, bool include_lca, Args... args) {
bool rev = false;
vector<pair<int, int>> down;
while (top[u] != top[v]) {
if (depth[top[u]] < depth[top[v]]) {
swap(u, v);
rev ^= 1;
}
int left = start[top[u]];
int right = start[u];
if (rev) {
down.emplace_back(left, right);
} else {
int res = range_ds.search_right_mutable(left, right, args...);
if (res != range_ds.lim) return preorder[res];
}
u = parent[top[u]];
}
if (include_lca || u != v) {
if (depth[u] < depth[v]) {
swap(u, v);
rev ^= 1;
}
int left = start[v] + !include_lca;
int right = start[u];
if (rev) {
down.emplace_back(left, right);
} else {
int res = range_ds.search_right_mutable(left, right, args...);
if (res != range_ds.lim) return preorder[res];
}
}
for (auto it = down.rbegin(); it != down.rend(); it++) {
int res = range_ds.search_left_mutable(it->first, it->second, args...);
if (res != range_ds.lim) return preorder[res];
}
return -1;
}
private:
int build(int u, int idx) {
in[u] = idx++;
start[u] = (int)preorder.size();
preorder.push_back(u);
if (!adj[u].empty()) {
pair<int, size_t> big;
for (size_t i = 0; i < adj[u].size(); i++) {
big = max(big, pair(subtree[adj[u][i]], i));
}
if (big.second > 0) {
swap(adj[u][0], adj[u][big.second]);
}
top[adj[u].front()] = top[u];
idx = build(adj[u].front(), idx);
for (size_t i = 1; i < adj[u].size(); i++) {
int v = adj[u][i];
top[v] = v;
idx = build(v, idx);
}
}
out[u] = idx++;
return idx;
}
};
template <class Node_t, typename Query_t, bool push = true, bool break_cond = false>
struct segment_tree {
int lim, length;
vector<Node_t> data;
Node_t& operator [] (int i) { return data[i]; }
segment_tree(int n): lim(n),
length(1 << (lim == 1 ? 0 : 32 - __builtin_clz(lim - 1))), data(2 * length) {}
template <class Input_t>
segment_tree(const vector<Input_t>& a, int offset = 0): lim((int)size(a)),
length(1 << (lim == 1 ? 0 : 32 - __builtin_clz(lim - 1))), data(2*length) {
for (int i = offset; i < lim; i++) {
data[length + i] = Node_t(a[i]);
}
build();
}
void build() {
for (int i = length - 1; i > 0; i--) {
data[i].pull(data[2*i], data[2*i + 1]);
}
}
void assign_lengths() {
for (int i = 0; i < length; i++) {
data[i + length].length = 1;
}
for (int i = length - 1; i > 0; i--) {
data[i].length = data[2 * i].length + data[2 * i + 1].length;
}
}
template <class... Args>
void update_range(int l, int r, const Args&... args) {
update(l, r, args...);
}
template <class... Args>
void update(int l, int r, const Args&... args) {
if (r < l) return;
if (l < 0 || lim <= r) throw invalid_argument("update range out of bounds");
__update(l, r, 1, 0, length - 1, args...);
}
template <class... Args>
void __update(int l, int r, int i, int first, int last, const Args&... args) {
if constexpr (break_cond) {
if (data[i].break_condition(args...)) return;
if (l <= first && last <= r && data[i].put_condition(args...)) {
return data[i].put(args...);
}
if (i >= length) {
throw invalid_argument("put_condition/break_condition is incorrect, "
"trying to descend past a leaf");
}
} else {
if (l <= first && last <= r) {
return data[i].put(args...);
}
}
if constexpr (push) data[i].push(data[2*i], data[2*i + 1]);
int mid = (first + last) / 2;
if(l <= mid) __update(l, r, 2*i, first, mid, args...);
if(mid < r) __update(l, r, 2*i + 1, mid + 1, last, args...);
data[i].pull(data[2*i], data[2*i + 1]);
}
template <class... Args>
Query_t query_range(int l, int r, const Args&... args) {
return query(l, r, args...);
}
template <class... Args>
Query_t query(int l, int r, const Args&... args) {
if (r < l) return Node_t::default_value();
if (l < 0 || lim <= r) throw invalid_argument("query range out of bounds");
return __query(l, r, 1, 0, length - 1, args...);
}
template <class... Args>
Query_t __query(int l, int r, int i, int first, int last, const Args&... args) {
if (l <= first && last <= r) return data[i].get(args...);
if constexpr (push) data[i].push(data[2*i], data[2*i + 1]);
int mid = (first + last) / 2;
if(r <= mid) return __query(l, r, 2*i, first, mid, args...);
if(mid < l) return __query(l, r, 2*i + 1, mid + 1, last, args...);
return Node_t::merge(
__query(l, r, 2*i, first, mid, args...),
__query(l, r, 2*i + 1, mid + 1, last, args...));
}
template <class... Args>
void update_point(int x, const Args&... args) {
if (x < 0 || lim <= x) throw invalid_argument("update_point index out of bounds");
__update_point(x, 1, 0, length - 1, args...);
}
template <class... Args>
void __update_point(int x, int i, int first, int last, const Args&... args) {
if (first == last) return data[i].put(args...);
if constexpr (push) data[i].push(data[2*i], data[2*i + 1]);
int mid = (first + last) / 2;
if (x <= mid) __update_point(x, 2*i, first, mid, args...);
else __update_point(x, 2*i + 1, mid + 1, last, args...);
data[i].pull(data[2*i], data[2*i + 1]);
}
template <class... Args>
Query_t query_point(int x, const Args&... args) {
if (x < 0 || lim <= x) throw invalid_argument("query_point index out of bounds");
return __query_point(x, 1, 0, length - 1, args...);
}
template <class... Args>
Query_t __query_point(int x, int i, int first, int last, const Args&... args) {
if (first == last) return data[i].get(args...);
if constexpr (push) data[i].push(data[2*i], data[2*i + 1]);
int mid = (first + last) / 2;
if (x <= mid) return __query_point(x, 2*i, first, mid, args...);
else return __query_point(x, 2*i + 1, mid + 1, last, args...);
}
template <class... Args>
void update_up(int x, const Args&... args) {
static_assert(!push);
if (x < 0 || lim <= x) throw invalid_argument("update_up index out of bounds");
for (int i = x + length; i > 0; i /= 2) {
data[i].put(args...);
}
}
template <class... Args>
Query_t query_up(int x, const Args&... args) {
if (x < 0 || lim <= x) throw invalid_argument("query_up index out of bounds");
return __query_up(x, 1, 0, length - 1, args...);
}
template <class... Args>
Query_t __query_up(int x, int i, int first, int last, const Args&... args) {
if (first == last) return data[i].get(args...);
if constexpr (push) data[i].push(data[2*i], data[2*i + 1]);
int mid = (first + last) / 2;
if (x <= mid) {
return Node_t::merge(data[i].get(args...), __query_up(x, 2*i, first, mid, args...));
} else {
return Node_t::merge(data[i].get(args...), __query_up(x, 2*i + 1, mid + 1, last, args...));
}
}
template <class... Args>
int search_left(int l, int r, Args... args) {
if (r < l) return lim;
if (l < 0 || lim <= r) throw invalid_argument("search_left range out of bounds");
return __search_left(l, r, 1, 0, length - 1, forward_as_tuple(args...));
}
template <class... Args>
int search_left_mutable(int l, int r, Args&... args) {
if (r < l) return lim;
if (l < 0 || lim <= r) throw invalid_argument("search_left range out of bounds");
return __search_left(l, r, 1, 0, length - 1, forward_as_tuple(args...));
}
template <class... Args>
int __search_left(int l, int r, int i, int first, int last, tuple<Args&...> args) {
if (l <= first && last <= r
&& !apply(&Node_t::contains, tuple_cat(tuple(data[i]), args))) return lim;
if (first == last) return first;
if constexpr (push) data[i].push(data[2*i], data[2*i + 1]);
int mid = (first + last) / 2;
int res = (l <= mid ? __search_left(l, r, 2*i, first, mid, args) : lim);
if (res == lim && mid < r) res = __search_left(l, r, 2*i + 1, mid + 1, last, args);
return res;
}
template <class... Args>
int search_right(int l, int r, Args... args) {
if (r < l) return lim;
if (l < 0 || lim <= r) throw invalid_argument("search_right range out of bounds");
return __search_right(l, r, 1, 0, length - 1, forward_as_tuple(args...));
}
template <class... Args>
int search_right_mutable(int l, int r, Args&... args) {
if (r < l) return lim;
if (l < 0 || lim <= r) throw invalid_argument("search_right range out of bounds");
return __search_right(l, r, 1, 0, length - 1, forward_as_tuple(args...));
}
template <class... Args>
int __search_right(int l, int r, int i, int first, int last, tuple<Args&...> args) {
if (l <= first && last <= r
&& !apply(&Node_t::contains, tuple_cat(tuple(data[i]), args))) return lim;
if (first == last) return first;
if constexpr (push) data[i].push(data[2*i], data[2*i + 1]);
int mid = (first + last) / 2;
int res = (mid < r ? __search_right(l, r, 2*i + 1, mid + 1, last, args) : lim);
if (res == lim && l <= mid) res = __search_right(l, r, 2*i, first, mid, args);
return res;
}
};
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
template <typename T>
using ordered_set = __gnu_pbds::tree<T,
__gnu_pbds::null_type,
less<T>,
__gnu_pbds::rb_tree_tag,
__gnu_pbds::tree_order_statistics_node_update>;
using ll = long long;
using ld = long double;
using pt = complex<ld>;
constexpr char nl = '\n';
constexpr int INF = 0x3f3f3f3f;
constexpr ll INFLL = 0x3f3f3f3f3f3f3f3f;
constexpr int MOD = 998244353;
constexpr ld EPS = 1e-9L;
random_device _rd; mt19937 rng(_rd());
struct node {
int value; bool lazy;
node() = default;
void put(int v) { value = v; lazy = true; }
int get() const { return value; }
void push(node& a, node& b) {
if (lazy) {
a.put(value);
b.put(value);
lazy = false;
}
}
void pull(const node&, const node&) const {}
};
using DS = segment_tree<node, int>;
ll sqr(int x) { return (ll)x*x; }
int main() {
cin.tie(0)->sync_with_stdio(0);
cout << fixed << setprecision(10);
#if defined(ONLINE_JUDGE) && defined(FILENAME)
freopen(FILENAME ".in", "r", stdin);
freopen(FILENAME ".out", "w", stdout);
#endif
int T;
cin >> T;
while(T--) {
int n;
cin >> n;
vector<int> parent(n+1);
vector<vector<int>> adj(n+1);
for(int i=2; i<=n; i++) {
cin >> parent[i];
adj[parent[i]].push_back(i);
}
range_query_tree<DS, int> tree(move(adj), 1);
vector<int> down(n+1), tail(n+1);
vector<ll> ans(n+1);
tree.update_point(1, 1);
tail[1] = 1;
ans[1] = 0;
for(int i=2; i<=n; i++) {
tree.update_point(i, i);
tail[i] = i;
ans[i] = ans[i-1];
int head = i;
while (head != 1) {
int mid = parent[head];
int top = tree.query_point(mid);
if (tree.depth[i] <= tree.depth[tail[top]]) {
break;
}
if (mid == tail[top]) {
down[mid] = i;
tail[top] = i;
tree.update_point(i, top);
ans[i] += sqr(tree.depth[i] - tree.depth[top]) - sqr(tree.depth[mid] - tree.depth[top]);
} else {
ans[i] -= sqr(tree.depth[i] - tree.depth[head]) + sqr(tree.depth[tail[top]] - tree.depth[top]);
ans[i] += sqr(tree.depth[i] - tree.depth[top]) + sqr(tree.depth[tail[top]] - tree.depth[down[mid]]);
tree.update_path(tail[top], down[mid], true, down[mid]);
tree.update_path(i, head, true, top);
tail[down[mid]] = tail[top];
tail[top] = i;
down[mid] = head;
}
head = top;
}
}
for(int i=1; i<=n; i++) {
cout << ans[i] << " ";
}
cout << nl;
}
return 0;
}
Comments